混沌序列
最近做信息安全方面的项目,看到一些关于混沌变换的论文,总结一番。
关于混沌
如果一个系统的演变过程对初始的状态十分敏感,就把这个系统称为是混沌系统。
在1972年12月29日,美国麻省理工教授、混沌学开创人之一E.N.洛仑兹在美国科学发展学会第139次会议上发表了题为《蝴蝶效应》的论文,提出一个貌似荒谬的论断:在巴西一只蝴蝶翅膀的拍打能在美国得克萨斯州产生一个龙卷风,并由此提出了天气的不可准确预报性。至此以后,人们对于混沌学研究的兴趣十分浓厚,今天,伴随着计算机等技术的飞速进步,混沌学已发展成为一门影响深远、发展迅速的前沿科学。
混沌来自于非线性动力系统,而动力系统又描述的是任意随时间变化的过程,这个过程是确定性的、类似随机的、非周期的、具有收敛性的,并且对于初始值有极敏感的依赖性。而这些特性正符合序列密码的要求。19**Robert Matthews在Logistic映射的变形基础上给出了用于加密的伪随机数序列生成函数,其后混沌密码学及混沌密码分析等便相继发展起来。混沌流密码系统的设计主要采用以下几种混沌映射:一维Logistic映射、二维He’non映射、三维Lorenz映射、逐段线性混沌映射、逐段非线性混沌映射等,在本文中,我们主要探讨一维Logistic映射的一些特性。
一、单logistic混沌映射
一维Logistic映射从数学形式上来看是一个非常简单的混沌映射,早在20世纪50年代,有好几位生态学家就利用过这个简单的差分方程,来描述种群的变化。此系统具有极其复杂的动力学行为,在保密通信领域的应用十分广泛,其数学表达公式如下:
Xn+1=Xn×μ×(1-Xn) μ∈[0,4] X∈(0,1) 部分文章写为X∈[0,1] 是有误的
其中 μ∈[0,4]被称为Logistic参数。研究表明,当X∈[0,1] 时,Logistic映射工作处于混沌状态,也就是说,有初始条件X0在Logistic映射作用下产生的序列是非周期的、不收敛的,而在此范围之外,生成的序列必将收敛于某一个特定的值。如下图所示:
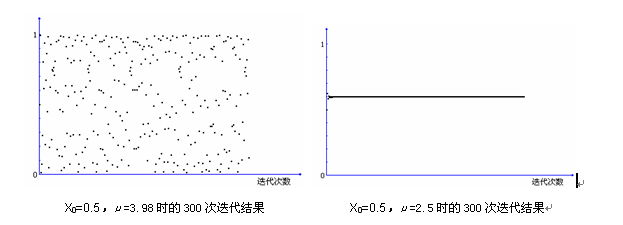
可以看出,在μ的取值符合3.5699456<μ<=4的条件,特别是比较靠近4时,迭代生成的值是出于一种伪随机分布的状态,而在其他取值时,在经过一定次数的迭代之后,生成的值将收敛到一个特定的数值,这对于我们来说是不可接受的。
下图中描述了X0值一定时,对于不同的μ的取值,迭代可能得到的值:
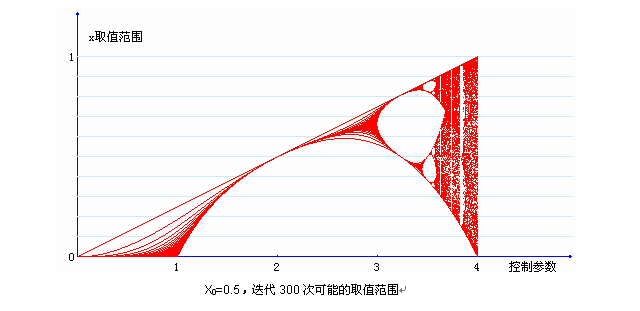
从图中我们可以看出,在_μ_越接近4的地方,X取值范围越是接近平均分布在整个0到1的区域,因此我们需要选取的Logistic控制参数应该越接近4越好。在01之间次好,在13.5之间的效果很不好。
在_μ_的值确定之后,我们再来看看初始值X0对整个系统的影响。刚才也说过了,混沌系统在初始值发生很小变化时,得到的结构就会大相径庭,在Logistic混沌映射中也是如此。
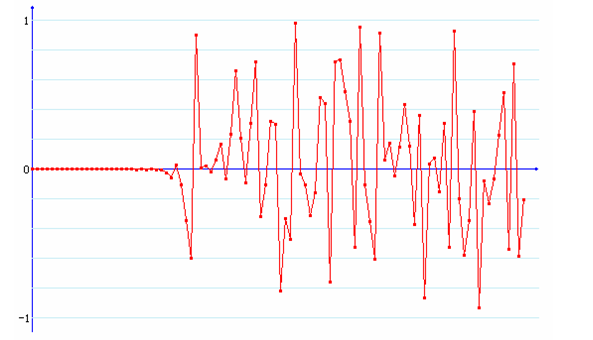
上图显示的是X0= 0.663489000和X0= 0.663489001,μ=3.99时两个Logistic序列之差的图像,很明显,在最开始20多次迭代,两者的差很小,近似等于0,但随着迭代次数的增加,两个序列的值显示出一种无规律的情形,两者相差也比较大了。因此可以看出该系统具有很好的雪崩效应。
我们在使用Logistic混沌系统时,可以先让系统先迭代一定次数之后,再使用生成的值,这样可以更好地掩盖原始的情况,使雪崩效应扩大,这样可以具有更好的安全性。
最后我们再来看看Logistic的随机分布特性,一个好的伪随机序列应该有比较平均的分布,也就是说,每个数出现的概率应该是相等的。我们对X0=0.2,μ=3.9999的Logistic混沌映射进行30000次迭代后对其值进行统计,分布情况如下表所示:
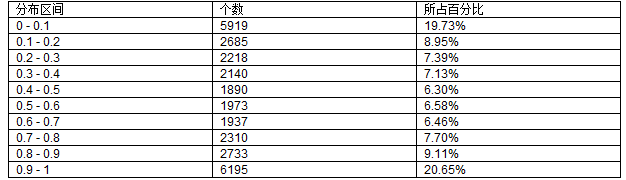
从上表中我们可以看出,Logistic映射的迭代序列的分布并不是均匀的,对于其他的X0取值也有类似的结构。而且从表中我们还可以看出,其分布是一种两头大中间小的情形。虽然分布情况并不是很平均,但是对于一般情形来说,Logistic映射序列是可以满足我们的需求的。而且我们可以对其想办法加以改进,使之可以获得更好的平均性。
二、超混沌序列
超混沌是一类特殊的混沌现象,它和混沌相比具有更多方向的不稳定性。一般,系统的状态变量愈多,可能出现不稳定的程度就愈高。所以,从实际应用的角度考虑,更希望用超混沌序列作为随机码来提高系统的安全性;但采用高维系统产生超混沌序列较之低维系统计算更复杂,实际应用中通常寻找系统状态变量参数尽可能少的超混沌系统。
二维超混沌离散系统一般有如下形式:
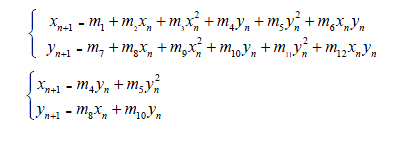
其中,(i=1, 2,?, 12)为待定常系数。第二组公式为简单二维超混沌系统
对比超混沌和单logistic混沌
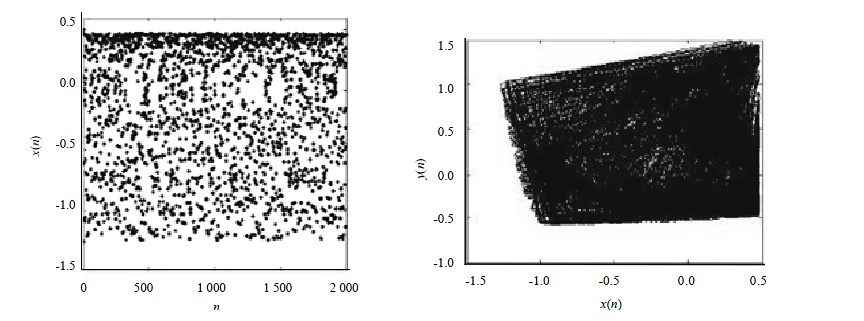
左图为logistic混沌映射分布图,右图为超混沌分布。在仿真实验中,先固定m5= −1.2, m8= −1.1, m10 =0.1;经多次实验发现,当m4 =1.52时,系统已经进入超混沌状态。公式为:
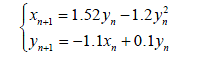
由此可看出,超混沌在一定空间下的离散型表现的非常好。
三、cat映射和logistic映射
cat映射是一个二维的可逆混沌映射,其动力学方程的一般形式如:
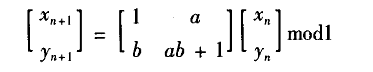
当a b均为1时,就是经典的Amold Cat映射.cat映射具有较好的混沌特性,其每次的运算首先将正方形的点空间线性拉伸,然后通过模运算分割折叠。
基于cat映射和单logistic映射Xn+1=Xn×μ×(1-Xn) μ∈[0,4] X∈(0,1)
推导出改进的logistic映射,其动力学方程
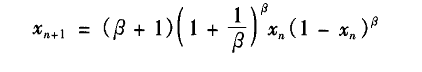
其中β为[1,4]之间的一个实数,X。∈ (0,1) 分析发现所得到的随机序列与原始随机序列平均有99.9999% 不相同.
与此得出这种混合映射方式产生的离散序列具有更好的效果。
四、双logistic映射的生成
前面已经知道单logistic映射Xn+1=Xn×μ×(1-Xn) μ∈[0,4] X∈(0,1)在μ趋近于4的时候产生的序列通向混沌。
令C1(μ1,x1, n1),C2(μ2,x2,n2)为单logistic 映射的不同参数,表示为在u,x下产生的混沌序列中取n位组成的混沌序列子集。
得到 C1 = { xn1 ,xn1+1 , ?, xn1+m1 - 1 } , C2 = { yn2 , yn2+1 , ?, yn2+m2 - 1 }
其中m1和m2表示需要应用的二维事件的行数与列数,例如数据库的行列,图像的行列。
非线性映射函数f 和g k 的定义如下:
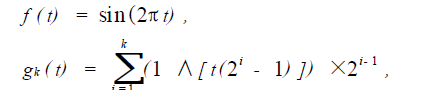
其中, t ∈R , k = 1 ,2 , ?; f ( t) 为f : t ->[ - 1 ,1 ] 的映射; gk ( t) 为gk : t ->{ 0 ,1} k 的映射. 利用映射f 和gk 分别从C1 和C2 中各映射出两组实值序列,记为:Cx 1 、Cx 2 、Cy1 和Cy2 ,且:
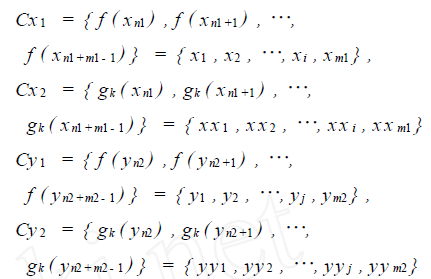
其中: xi = f ( xn1+i- 1 ) ; xxi = gk ( xn1+i - 1 ) ; yj =f( yn2+ j - 1 ) ; yy j = gk ( yn2+ j - 1 ) ;
i = 1 ,2 , ?, m1 ; j =1 ,2 , ?, m2 .
双logistic通过针对二维事物来产生两组混沌序列,通过新的非线性映射结合起来,离散程度高,但是计算相对复杂了。